线性DP
1.LIS问题
定义:求出最长上升子序列。即
$$
B\subseteq A,B[i]<B[j]\ \ (i < j)
$$
实现:
1. $O(n^2)$
思路:依题意模拟。
$$
F[i]=max_{0\le j<i,a[i]<a[j]}{F[j]+1}
$$
code:
1
2
3
4
5
6
7
8
9
10
| void dp()
{
for(int i = 1;i <= n;i++)
{
f[i] = 1;
for(int j = 1;j < i;j++)
if(a[i] > a[j])
f[i] = max(f[i],f[j] + 1);
}
}
|
2.$O(n\log n)$
思考优化方法。设 D[i] 为以 a[i] 结尾的最长上升子序列长度, g[j] 为 D[i] = j 中最大的 i ,易知 g[i] 单增。
对于每个 a[i] 二分查找最小的k使得 g[i]>a[i] ,则 d[i]=k ,更新 g[i]
说人话:就是算出长度为 l 的前缀最后一位最小是几。如果这位能接上,就更新答案
code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| int search(int l,int r,int val,int k)
{
while (l < r)
{
int mid = (l + r) >> 1;
if(cmp(g[mid],val,k)) l = mid + 1;
else r = mid;
}
return l;
}
void DP()
{
memset(g,0x7f,sizeof(g));
ans = -1;
for(int i = 1;i <= n;i++)
{
f[i] = search(1,i,a[i],2);
g[f[i]] = min(g[f[i]],a[i]);
if(f[i] > ans) ans = f[i];
}
}
|
2.LCS问题
定义:最长公共子序列。
1.标准做法$O(n^2)$
$$
F[i] = max{F[j] + 1}(s_1[i] == s_2[i] )
$$
$$
F[i]=max{F[j]}(s_1[i]\ne s_2[i])
$$
code:
1
2
3
4
5
6
7
8
9
10
11
12
13
| int f[N];
char s1[N],s2[N];
void DP()
{
for(int i = 1;i <= n;i++)
for(int j = 1;j < i;j++)
{
if(s1[i] == s2[i])
f[i] = max(f[i],f[j] + 1);
else
f[i] = max(f[i],f[j]);
}
}
|
2.优化 $O(n\log n)$
考虑转化。
将 LCS 转化为 LIS 。将 A 中元素编号为 1~n+1 ,在 B 中将 A 中出现的过的元素改为对应标号。没出现的编为 0
code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
map<int,int>M;
int main()
{
int n,m,p,q,i,k,j,t;
int a[66000],b[66000],g[66000];
cin>>t;
for(int test=1;test<=t;++test)
{
M.clear();
int x=1;
cin>>n>>p>>q;
for(i=1;i<=p+1;++i)
{
scanf("%d",a+i);
if(!M[a[i]]) M[a[i]]=x++;
}
for(i=1;i<=q+1;++i)
{
scanf("%d",b+i);
b[i]=M[b[i]];
}
memset(g,inf,sizeof(g));
for(i=1;i<=q+1;++i)
{
*lower_bound(g,g+65000,b[i])=b[i];
}
printf("Case %d: %d\n",test,(int)(lower_bound(g,g+65000,inf)-g));
}
return 0;
}
|
区间DP
定义:以区间长度为阶段,以左右端点划分状态。
常用做法:
1
2
3
4
5
6
7
| for(int len = 2;len <= n;len++)
for(int i = 1;i + len - 1<= n;i++)
{
int j = i + len - 1;
for(int k = i;k <= j;k++)
}
|
先推方程。设计 F[i][j] 表示将 i 到 j 堆石子合并所获得的最大权值, sum[i] 为前缀和。显然有:
$$
F[i][j]=max{F[i][k] +F[k][j]+sum[j] - sum[i - 1]}(k \in [i,j])
$$
所以就可以写出下面的代码:
1
2
3
4
5
6
7
8
9
10
| for(int len = 1;len < n;len++)
{
for(int i = 1,j;i + len <= n * 2;i++)
{
j = i + len;
f[i][j] = 0;
for(int k = i;k < j;k++)
f[i][j] = max(f[i][j],f[i][k] + f[k + 1][j] + sum[j] - sum[i - 1]);
}
}
|
最小值同理。
这里有一个小技巧:
原题是在环上处理的。很容易发现在环上处理是非常困难的,所以我们把环打开为链,并复制两遍,即可解决问题。即:
1
2
3
4
5
| for(int i = 1;i <= n;i++)
{
scanf("%d",&a[i]);
a[i + n] = a[i];
}
|
code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| #include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
const int N = 210;
int f[N][N];
int a[N];
int sum[N];
int main()
{
int n;
scanf("%d",&n);
for(int i = 1;i <= n;i++)
{
scanf("%d",&a[i]);
a[i + n] = a[i];
}
for(int i = 1;i <= n * 2;i++)
sum[i] = sum[i - 1] + a[i];
for(int len = 1;len < n;len ++)
{
for(int i = 1 , j;i + len <= n * 2;i++)
{
j = i + len;
f[i][j] = (1 << 28);
for(int k = i;k < j;k++)
f[i][j] = min(f[i][j] , f[i][k] + f[k + 1][j] + sum[j] - sum[i - 1]);
}
}
int ans = 1 << 28;
for(int i = 1;i <= n + 1;i++)
ans = min(f[i][i + n - 1],ans);
printf("%d\n",ans);
memset(f,0,sizeof(f));
for(int len = 1;len < n;len++)
{
for(int i = 1,j;i + len <= n * 2;i++)
{
j = i + len;
f[i][j] = 0;
for(int k = i;k < j;k++)
f[i][j] = max(f[i][j],f[i][k] + f[k + 1][j] + sum[j] - sum[i - 1]);
}
}
ans = 0;
for(int i = 1;i <= n + 1;i++)
ans = max(ans,f[i][i + n - 1]);
printf("%d",ans);
return 0;
}
|
斜率优化
先考虑暴力怎么做。设$s_i$为$c_i$的前缀和。容易知道:
$$
f[i] = min{f[j] + (s[i] - s[j] + i - j - 1 - L)^2}
$$
复杂度:$O(n^2)$
考虑优化。
将柿子展开。令$b_i=s_i + i$,$j$为最佳决策点。有:
$$
f[i]=f[j]+(b_i-b_j-(L+1))^2
$$
展开,移项:
$$
f[j]+(b[j]+L+1)^2 = 2b[j]b[i]+2Lb[i]-b[i]^2
$$
若设 $f[j]+(b[j]+L+1)^2$为纵坐标,$b[i]$为横坐标,原式变成了一条直线。
$$
l:y=2b[j]x+2Lb[i]-b[i]^2
$$
斜率是$2b[j]$,截距为$2Lb[i]-b[i]^2$
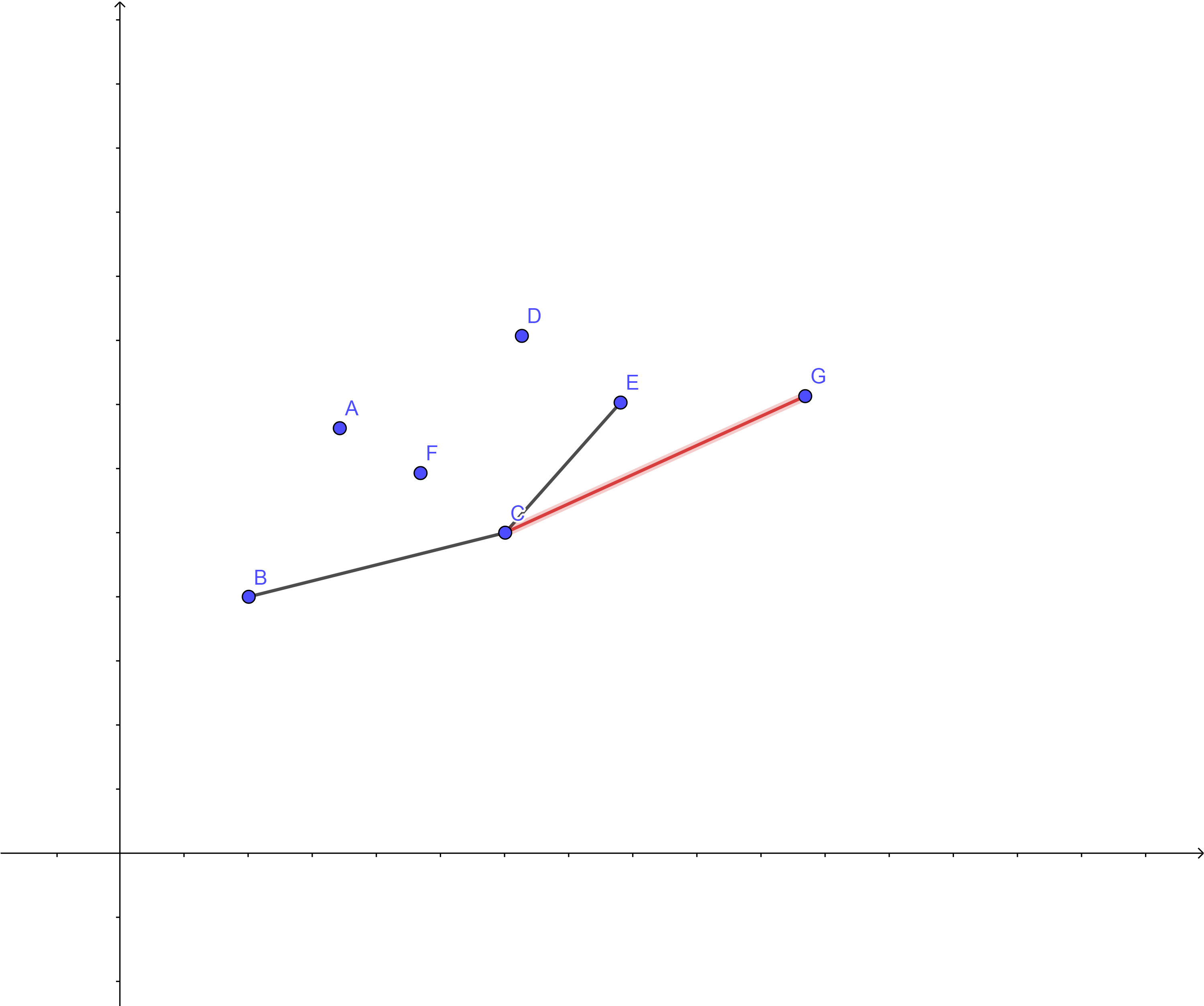
(图源:https://www.cnblogs.com/15owzLy1-yiylcy/p/11336510.html)
利用线性规划思想。从下往上平移直线。第一个碰到的点则为最优的$j$。
维护一个凸壳。
1
2
3
4
5
| 上图中,决策点的下凸壳为 (B,C,E),但因为加入了点 G,点 E 死了(大雾。
可以得到如下结论:
1、凸壳上边的斜率是从左到右单调递增的,否则会出现上图的情况。
2、设凸壳上的点从左至右依次记为 1~k,显然有:在凸壳中加入一个横坐标大于当前所有点的点 t,若 slope(k−1,t)≤slope(k−1,k),则 k 不在凸壳上。
依照上述做法可以用单调队列来维护凸壳。 ---15owzLy1
|
(具体维护见代码)
code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| #include<stdio.h>
#include<algorithm>
using namespace std;
long long queue[50010],head = 1,tail = 1;
long long n,l;
long long c[50010],s[50010],f[50010],b[50010];
double calc_y(long long x)
{
return f[x] + (b[x] + l + 1) * (b[x] + l + 1);
}
double calc_k(long long x,long long y)
{
return (calc_y(y) - calc_y(x)) / (double)(b[y] - b[x]);
}
int main()
{
scanf("%lld %lld",&n,&l);
for(int i = 1;i <= n;i++)
scanf("%lld",&c[i]),s[i] = s[i - 1] + c[i],b[i] = s[i] + i;
for(int i = 1;i <= n;i++)
{
while(tail != head && calc_k(queue[head],queue[head + 1]) < 2 * b[i]
head++;
int j = queue[head];
f[i] = f[j] + (b[i] - b[j] - l - 1) * (b[i] - b[j] - l - 1);
while(tail != head && calc_k(i,queue[tail - 1]) < calc_k(queue[tail - 1],queue[tail]))
tail--;
queue[++tail] = i;
}
printf("%lld\n",f[n]);
return 0;
}
|
习题:
[NOI2019] 回家路线
(明天写)
